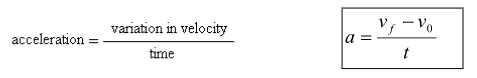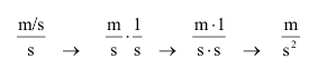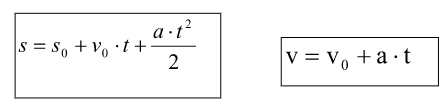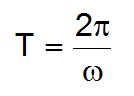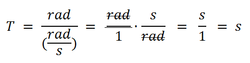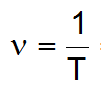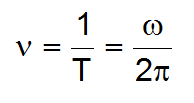Unit 6 - Movement
|
Key concept - Change- Past of an object in motion can be reconstructed and future foreseen on the basis of the current state and the forces acting upon it
Related concepts - Patterns and Motion- Motion and forces can be expressed in mathematical equations Global concept - Scientific and Technical Innovation- Constant parallel improvement of science and technology can provide answers to some of human questions about the universe.. |
|
|
|
Pre-knowledge
Task 6i: Complete the following LINK to see what you can remember from previous years.
Task 6ii: Complete the basic terms quiz below:
Task 6 iii: The ability to rearrange equations is essential in this topic Complete the questions below on a piece of paper:
|
|
|
| ||
6a - Magnitudes for describing movement
|
Body - The name for the moving object.
Origen - A reference point that allows us to describe the position of a body. Position or space (s) - Is the place where the body is positioned in relation to the origen. Displacement (sf-so)- The distance between 2 positions. Speed - The average speed can be calculated using speed = distance/time. |
Velocity (v) - This is the speed of something but given with a specific direction e.g. 10 m/s north. Quantities like this are called "vectors" as they have a magnitude and a direction.
Acceleration (a) - We say something is accelerating if its velocity is changing. Uniform movement - covers the same space in equal periods of time. Varied movement - different amounts of space are covered in equal periods of time. |
6b - Reference system
When studying movements it is always necessary to establish a reference system. We usually consider this a static point, the beginning of the movement or, when convenient, just ourselves.
|
|
Just changing the reference system form Earth to Sun the solar system was simpler to understand
Thinking question: How many reference points can you think of when Mr Canning throws a ball out of a window?
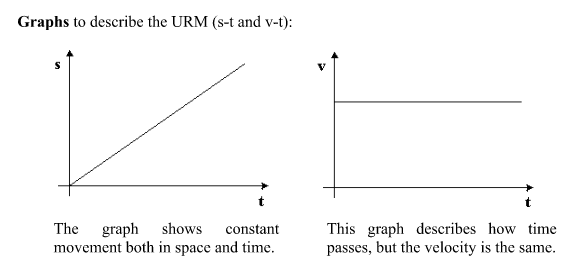
6c - Uniform rectilinear motion (URM)
A motion which covers equal distances in the equal intervals of time is called "uniform" and "rectilinear" means that the body is travelling a straight line.
|
The first graph shows that the space (s) between positions of a body is consistent over equal periods of time.
|
The second graph shows that velocity remains uniform over time.
|
Formulas
velocity = change in position / time v = (sf - s0) / t
position = initial position + (velocity · time) s = so + (v·t)
velocity = change in position / time v = (sf - s0) / t
position = initial position + (velocity · time) s = so + (v·t)
Task 6c i: Complete these simple URM questions. LINK
Galileo Gallei - 1564-1642
|
|
6d - Uniformly accelerating rectilinear motion (UARM)
The accelerated movement is a movement in which velocity changes with time. If there is an increase in velocity, the acceleration is positive and If the velocity diminishes, the acceleration is negative (deceleration).
If we apply the formula above to the International System, we see that acceleration is about how many m/s velocity increases or decreases each consecutive second.
Consequently, the unit of acceleration in the International System is m / s^2 .
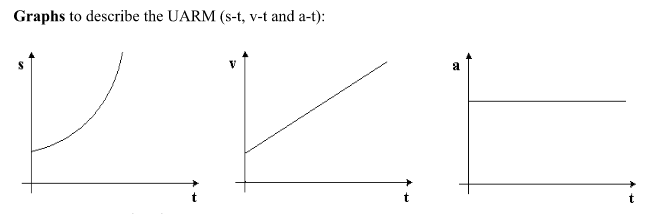
UARM is the uniform acceleration of a body in a straight line.
|
The Graph 1 shows that during the movement, more space is covered in less time.
|
Graph 2 shows velocity increasing uniformly over time.
|
Graph 3 shows the uniform (constant) acceleration.
|
Formulas
|
Lab session 8: In the reference system of our investigation, Vo was always 0 m/s and So was 0 m. Therefore the equations can be written as they are below.
|
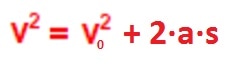
When the two previous equations are combined with time the equation is
|
Directly proportional graphs
When plotting a graph of "Y" against "X", where "c" is a constant: Y = c · X It will be a straight line graph with a gradient of "c". |
|
Task 6d ii: Complete the following problems on UARM.
| uarm_exercises_solved.doc |
| uarm_exercises.doc |
Extension:
|
Stats for Baumgartner´s jump:
Calculate his:
a) acceleration during freefall b) maximum speed c) theoretical maximum speed without air resistance |
|
6e - Uniform circular motionIn a circular movement the distance between the centre and the circumference (radius) is always the same. For this reason we must change our definition of position. We are now going to use the angle from the the x-axis (φ) to define position (pronounced "phi").
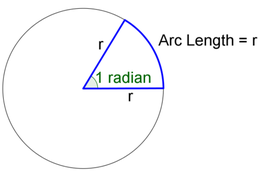
In physics, when using angles, we deal with radians (rad) instead of degrees (º). 
|
 KEY POINT: 360 º = 2π rad
If we need to convert from degrees to radians, we can use the rule of 3 with this conversion.
This is because it allows use to more easily link the angle with the length of the arch (L).
An angle of 1 rad --> Length of arch is 1 radius |
Symbols and units
KEY POINT: Position is defined as angle from the x-axis - φ in units radians
As we are now talking about circular motion, we cannot calculate the distance covered using sf - so. The space covered by the body will now be defined along the length of the arc, L. To calculate this we only need to know the angle, (φ) between the 2 positions and the radius (R).
KEY EQUATION: L = φ·R (L is the equivalent to space covered)
As we must now consider velocity in circular motion, we call it angular velocity (ω). As we now define position in terms of angle, the units for ω are given in rad/s.
KEY POINT: Angular velocity = ω in units = rad/s
By replacing the equation used in UARM....
sf = so + (v·t)
...with those seen in circular motion, we can form the following equation
KEY EQUATIONS:
φf = φo + (ω·t)
6f - Period and frequency (UCM)
As circular movements are repeated at regular intervals, it is useful to have expressions for:
- The time taken to complete one full revolution of the circle --> Period (T) in sec (s)
|
This is effectively "time = distance / speed". The units used in this equation (left) are
|
- The number of revolutions per second --> Frequency (v) in 1/s or Hz
|
Substituting the formula for T above--> |
|
Task 6e/f i. UCM problems
1. During their physics field trip to the amusement park, Tyler and Maria took a rider on the Whirligig. The Whirligig ride consists of long swings which spin in a circle at relatively high speeds. As part of their lab, Tyler and Maria estimate that the riders travel through a circle with a radius of 6.5 m and make one turn every 5.8 seconds. Determine the velocity, angular velocity of the riders on the Whirligig and the frequency, v.
2. A Ferris wheel has a diameter of 150 meters and takes approximately 30 minutes to make a full circle. Determine the velocity and angular velocity of the riders on the Singapore Flyer. And the frequency?
3. During the spin cycle of a washing machine, the clothes stick to the outer wall of the barrel as it spins at a rate of 1800 revolutions per minute. The radius of the barrel is 26 cm.
a. Calculate the period, T, when travelling at its maximum velocity.
b. Determine the angular velocity of the clothes.
a. Calculate the period, T, when travelling at its maximum velocity.
b. Determine the angular velocity of the clothes.
4. The merry-go-round at Eldridge Park takes riders on a spin at 8.0 m/s. The radius of the circle about which the outside riders move is 7.4 m.
a. Determine the period for the outside riders to make one complete circle.
b. Determine the angular velocity.
a. Determine the period for the outside riders to make one complete circle.
b. Determine the angular velocity.
Answers: 1. 7 m/s, 1.08 rad/s, 0.17 Hz; 2. 0.26 m/s, 0.0035 rad/s, 0.0035 Hz; 3.a. 0.033 s b. 188 rad/s; 4.a. 5.8 s b. 1.1 rad/s
Revision
URM
1. 9 practice questions (Google Doc) - LINK
UARM
1. 10 practice questions (Google Doc) - LINK
2. 20 practice questions (Physics classroom) - LINK
3. 7 more practice questions (Google Doc) - LINK
4. Level 7-8 questions - LINK
